岐阜市立長良東小学校 第１２回研究発表会 参加報告
文責 土 井
以下の記録は、土井が参加しながらモバイルで記録したものです。当然、言葉足らずのもの、誤解があるかもしれませんが、学校や授業者には全く責任はありません。ご了承ください。
平成１７年１０月２７日（木）８時２０分到着。ずいぶん早く到着したが、すでに受付は始まっていた。長良東小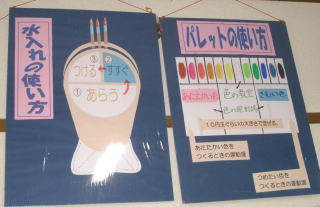
学校はこれで５回目か。ここ数年、毎年のように参観している。校舎内に入ると清掃中であった。素直な「おはようございます」のあいさつが気持ちいい。工作室で時間を過ごすが、手作りの掲示がすばらしい。写真を撮りまくる。
掃除終了の放送では、放送管理部の子が「○○さんと○○さんは・・・と言っていました。」と、掃除の感想を取材し、放送していた。「担当は、（放送局名）○○でした。」と、ラジオ放送のようである。こういう放送が好きだ。
控え室で紀要に目を通す。
研究主題は「自ら求めみがき合って高まる学習の創造」
この研究主題は開校以来変わらない。これまでに見た限りでは、すでにほとんどできあがっているといってよい。「みがき合い」という点では、日本でトップレベルであろう。さらに高いレベル追究が楽しみだ。
願う子どもの姿が、「自ら課題をもち、学び方を身に付け、仲間と切磋琢磨しながら課題解決に立ち向かい、高まっていく姿」とある。確かに、このような子どもたちを、毎年見てきた。
願う子どもの姿とかけ離れた？研究校を数多く見てきたが、ここまで一致している学校も珍しい。さすがに、一貫した目標を掲げているだけのことはある。職員の意識として、さらに子どもたちにまで定着しているのだろう。
事実上の研究主題は次のものである。
《共通視点》自己をみつめ確かな学力を身に付けていく子
この視点での実践が３年目になる。メタ認知的な自己評価能力をどのようにして育ててきたか、子どもたちの姿と教師の手だてを検証することを今日の課題としたい。
朝の会の様子を見て回る。同じような光景なのだが、どこか違う。何が？リラックスしている。のびのびしている。暖かな気持ちが素直にでる、自然な表現力がある。
今日は、第１時、２時を複数の教室を回り、第３時に渡辺先生の教室を見ることに決める。
学習公開１（9:15～10:00）
４年４組算数をのぞく。例によって、教室掲示はさしづめ算数教科教室のようだ。
磁石カードは４グループ。
１「めあてをつくるには」
わかっていること、きいていること、前とちがうところ、はっきりさせるには
２「考えをつくるには」
分度器、９０度、１８０度、３６０度 およそ、しき、0.1のいくつ分、リットル図を使って四捨五入を使って、数直線を使って、しきで、１度のいくつ分
３ 仲間にわかりやすくするには
つなげると、まとめると、もしも、いつでもいえる、かんたんにできる、前に使った考え方、
４ 「考え方を表現するには」
まず、つぎに、だだら
これらを駆使しながら、子どもたちが友達に説明しようとする。
今日の目当ては？「はい！」
「前の時間は９０度より大きな角を測ったので今日も測りたい」と言うと、「がんばってください」と周囲の子ども。学び合いは形から入っているが、心も育っている気がする。
これまでどんな勉強をしてきた？と教師が問う。「９０度より大きくて１８０度より小さい角度を測った」
これ何度ぐらい？「４５度」「９０度」本当？、確かめてみよう。これは？「１８０度」
そうだね。これは？この角度は何度でしょう？新しい課題だ。一斉に周囲と相談が始まる。学び合いのパターンだ。
挙手して指名された子が「前に出ます。」と言うと、他の子が「はい。」と応える。このテンポが流れるようである。
説明を始める。ここで「ちがうところ」のボードを使用した。これまでの学習との違いを明確にしている。次の子がまた前に出てきて
「『はっきりさせるには』分度器を使うといいと思います。」
そして次の子が「およそ」を貼り「２３０度 ぐらいだと思います。」
「２２０度ぐらいだと思います。」
教師が「どういうところをはっきりさせようか？」次々に言う子どもたち。指名すると「課題は、１８０度より多い角度を考えよう」これに対して一斉に「いいです。」
前時までとの違いをもとに全員で課題を明確にした。課題が決まった。プリントが配られ、作業が始まる。見事な流れだ。
ただ、流れすぎて、本当に全員が胸に落ちているかどうか、やや気になるところでもある。
ここで移動、
４年３組東っ子タイム
グループに分かれてゲストティーチャーの話を聞いている。受け身でない姿勢が子どもたちの問題意識を感じる。
３年３組英語
バッグの絵を見て、「There are seven bags.」と叫ぶ？子どもたち。英語に「ふれる」域を越えているので、１年生から積みあげられたものを感じる。
教師も英語で問いかける。７つのかばんに、それぞれ５つのクッキーが入っている
How many（ものの名前）in all?
かけ算の学習（算数）と英語が融合されている。パターン化しやすい算数は、確かに英語と組合せが可能だ。
（一つ分の大きさ）times（いくつ分）is（全体の大きさ）.So 全体の大きさ ものの名前．
かけ算の学習だ。式と答えを英語で言っている。
なるほど、楽しい英語を目指すだけでなく、英語を算数のかけ算という日常の学習の中に組み込んでいる。
６年３組の音楽 ふるさと ２部合唱
今年着任した専科の先生 だそうである。４グループに分かれて それぞれ合唱練習をしている。それぞれパートリーダーらしき子によるによるリードだ。教師は順に回りアドバイスをしている。
みんなで課題を出し合いながら楽譜に書き込んでいく。さらに歌を続ける。終わるとまた、次々に課題が出される。よく育った中学生レベルのパート練習だ。
その後発表会。感想が発表される。そのグループのめあてとの違いを指摘しているところが鋭い。毎回の拍手が温かい。
５年生東っ子タイム
３グループに分かれてのゲストティーチャーのはなしをきいている。児童の司会により次々に質問が出る。ただ、ややグループが大きすぎるか散漫にみえる。
３年２組東っ子タイム 竹林っていいな
先ほどはグループに分かれて聞いていたが、全体でまとめにはいっている。一人が発言すると、
「さっきにつなげて」と、前の発言に次々に付け足しながら発言している。よく聞いているからこそできることだ。この、人の意見をよく聞き、その意見にからめて考えを膨らませていく手法は、もしや？と思って周囲を見ると「社会科」の掲示。例の火事の掲示だ。
社会科の先生のクラスの子どもたちは、あいかわらずレベルが高い。発言をつなげることに関して、実によく鍛えられている。高め合おうと言う意識を感じる。
（カリキュラムの都合上、毎年火事の実践になってしまうのは少し残念だが、それは仕方がない。）
３年３組は英語の歌を手遊びを交えながら歌っている。
その後絵を見ながら 英語で式と答えを言っている。英語と教科学習を絡めながら、歌とゲームで英語に親しむ。なるほど。
学習公開２（10:15～11:00）
６年生道徳
ひろ子が正子から絵はがきをもらったという設定を説明。掲示し、こっち（定型）は５０円、こっちは定形外で１２０円かかることを説明。それだけで、「読みます。」短い導入がいい。いっせいにプリントを出し、鉛筆を持つ。
先生の声の大きさがいい。やや声量を抑えているので、子どもたちはより静粛になる。聞くための集中力が、目に見えるようである。
７０円の不足料金を相手に伝えるかどうかの内容だ。兄は伝えた方がよいという。母はお礼だけでよいという。
読み終えると早速作業にはいる。どうやら、登場人物の感情表現に線を引き、自分の気持ちを書き足しているように見える。
「はいどうぞ」 の声で手が上がる。
「ぼくは３０行目の７０円の不足を書きたくなかった。のところにこんな風な手紙はだめだよとかくと、どちらもいやな気持ちになるから書きたくなかったと思ったし、ぼくもそう思いました。」
「ちがうところです。」と挙手が上がる。
「４１行目の１２０円切手を書き足したと言うところで、他の人にも出すといけないからぼくは書きたします。」
「○○君に質問」などといいながら手が上がる。
発言の約束がよく徹底されている。
川田先生の教室へ行く
隣同士、英会話をしていた。板書には、「どこに住んでいるの？」
世界地図と動物の写真
A:I'm toki
B:I'm kiwi.
A: Where do you live ？
B: Ｉ live in New zealand｡
Where do you live?
A:Ｉ live in Japan.
代表の子が二人で会話をする。
今日は、これに出身地と好きなことを加えることをするそうだ。
福原愛は、北京に住み、日本出身で、卓球が好き。松井はニューヨークに住み、日本出身で、ベースボールが好き。同様に、ジーコ、朝昇竜、高橋尚子、ベッカム、ボブサップ。
会話の後、目を見ながら握手するところが本格的。
A:Hello，Ｉ'm ～。
B:Hello, Ｉ'm ～．
AB:Nice to meet you.
A:Where do you live？
B:Ｉlive in ～． I'm from～．
Ｉlike ～． Where do you live?
A:Ｉlive in ～. I'm from～．Ｉ like ～．
b:Ｉsee. Thank you.
女の子の発音がすばらしい。帰国子女かも？だとしたら、このように生かす手もあろう。 この後、交流が始まる。
１年音楽 はるなつあきふゆ 歌いながら身体表現している。金華山グループが発表。
終わるとさっそく感想を述べ合っている。１年生から一貫した学び会う姿勢はすばらしい。子どもたちはイントロから乗っている。そして歌詞による明確な表現の区別。さらに驚いたのは、伴奏が完全に終わるまで、余韻を大切にしている。これはなかなかできない。聴くことを大切にしている証拠だ。
最後にまた道徳会場へ。
吹き出しでまとめていたが、教室掲示を見て驚いた。こうしたアプローチの方法があった目か
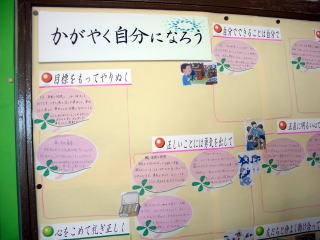
ら鱗が落ちる気がした。右壁には、徳目ごとに、これまでの授業での気づきを整理してある。背部には、一人一人の思いが掲示してある。
体育は授業を見ることができなかったが、掲示だけを見てもレベルの高さはすぐにわかる。
アンダーハンドパス、オーバーハンドパスについての指導が細かいステップを踏んで指導されている。また、今日の課題「相手のいないところをねらって打とう」も、写真をうまく使って説明している。
どの教科を見ても新鮮であり、進歩はめざましい。長良東小学校の授業は、毎年見ないと、進歩についていけない。
長良東小学校以外の学校現場は、果たしてどこまでついていっているのか？差が開くばかりでなければよいが・・・・
全体会 ここでは省略する
学習公開３（13:00～13:45）
前回、驚きの子どもたちを見せて頂いた、渡辺 出先生の算数クラスを訪問。授業前はどこにでもいる普通の子どもたち。緊張感は全く感じない。
チャイムを合図に、係生徒が２名前に出て一人を指名。一人の生徒が今日の目標を述べる。
各自が目標を持っている。その後、「起立」「はい！」「これから３時間目の算数の学習を始めます」「始めます」「礼」やや声が大きすぎる気がする。
教師が黒板に図を貼ると、「台形」と叫び、一斉に隣同士で何か言い始める。台形と判断した根拠を言っているのだろうか。
そして挙手。「この形は台形だと思います。なぜなら、一つの辺が平行だからです。どうですか？」①、「イエス！」さらに挙手が続く。
「私は前と比べて、前は長方形、正方形、平行四辺形、三角形の面積を求めたけど、今日は台形の面積を求めると思うけどどうですか。」②
さらに挙手が続く。指名される。
「私は頑張りたいことで、『式にしてみよう』、『前の考えを使えないか』『にている考えをつなげよう』を使って考えたいと思います。」③、「イエス！」
３人とも、磁石ボードを黒板に貼りながら説明している。
教師「ちょっと聞くけど、長方形、正方形、平行四辺形、三角形はどういう図形？」
一斉「面積が求められる図形」
教師「台形は？」
一斉「まだ、求められない」
教師「台形の面積を求めることができる？」多数「今までの考え方を使えばできる」
教師「ちょっと不安だなと言う人」少数が挙手
教師「じゃあ、似ている考えや、前の考えを生かしながら進めていきましょう。今日の課題は何にしよう？」
一斉「台形の面積の求め方を考えよう」
指名「台形の面積の求め方を考えよう」教師「じゃそれで行きましょう」
プリントを配布すると、先生や前の子から受け取り「ありがとう」と言う。学級経営がきめ細やかだ。ここまでたった４分間。密度がたいへん濃い。
各自でプリントで作業を始める。
教師は課題を板書すると、すぐに一人の子へアドバイスへ向かう。最初に支援が必要な児童を決めていたかのようだ。その後次々に机間指導。
プリントには二つの台形が書いてあり、２種類の方法で求積を考えさせている。
まわりながら教師は赤丸をつけている。
ちょうど１０分後、「じゃあやめてください。それでは発表できる人」ほとんど全員の手が上がる。それぞれ自分のやり方を「等積変形」「倍積変形」などと売り込んでいるのがすごい。それぞれ、前を向き、目から光線が出ているかのような力を感じる。
３人を指名。もちろん意図的である。３人は前でやるが、また「続きをやってください」
と続ける。さらに８分後の１時２３分。最初の子が説明を始める。
「ぼくは等積変形で考えました。この赤の部分をこっちにやって、青の部分をこっちにやると長方形ができますね。」一斉に「はい。」「そこで、縦×横をやると面積は２０平方センチメートルになります。どうですか？」「イエス！」
説明は、あくまでも他の子どもたちに向かって「～ですね。」とする。そして、他の子はそれに応える。これがこの学校全体のスタイル。
２人目。「私は台形はまだ求められないので、対角線を引いて考えました。ここに対角線を引くと、三角形が２つできますね。」「はい！」その後、それぞれの早な活計の面積を求めて合計していった。
３人目。「私は台形では求められないので、平行四辺形にして考えました。」と言い、自分の考えを説明した。
３人の説明を終えた後、教師の「どうですか？」の声に手が一斉に上がる。
最初の子に質問が出た。「○○君は長方形にして求めたが、それなら縦かける横でやる。しかし、底辺かける高さと平行四辺形の公式を使ったのはおかしいのでは？」という質問だ。
実に、他の児童の説明を細かい所まで聞いている。
これは、かけ算の交換法則や、長方形と平行四辺形の関係に関わる重要な問題なので、渡辺先生も食いついた。すぐに、「かけ算はひっくり返しても結果は同じなので、よいと思います」という意見が出る。２人目の子は、「紙を９０度回転させると縦横が変わるからこれでよい」と答えた。
それ以上が出なかったので、教師が「これ、平行四辺形じゃない？」と問いかけた。定義を確認した後、「平行四辺形って斜めじゃないとダメ？」「うん」この辺りは既成概念ができてしまっている。面白い所だが、教師は、定義に照らし合わせて「長方形は平行四辺形の仲間です」とまとめた。時間がないのでつっこめなかったのだろう。
「ほかにどうですか？」一斉に手が上がった中から一人の子が指名される。
「３つをつなげると、長方形、三角形、平行四辺形と、求められる形を利用して求めているという共通点があると思う。」と答えた。さらに次の子が、「横の長さと縦の長さを使っている」、しかし、「公式は・・・・」
「個人課題を公式にした人？」数人手が上がる。一人を指名。「わたしは、倍積変形にして考えました。台形をもう一つこっちにくっつけると平行四辺形になりますね。・・・・」
数字で面積を求める式を説明し、その後で、数字の意味を説明することで、公式の形にしていった。論理的に説明する力が育っている。誰もが育っているから素晴らしい。
「だから、（下底＋上底）×高さ÷２ になると思いますがどうですか？」に対して、型どおりの「イエス！」ではなく、「あっ、そういうことか」とつぶやきながら首を縦に振ってうなずく子の多いことも印象的だ。
さらに別の子が、ふたつめの図形を指しながら、「私はこの図形を使って公式を求めました」と言いながら、台形を対角線で２つの三角形に分け、それぞれの求積の式を合わせると、台形の公式になることを論理的に説明していった。
続いて、ひとつ目の図で、教師が「この１０って何だろう？」と言うと、多くの子が「分かった」と言って手を挙げ、等積変形でも、同じように公式にできることを、これまた論理的に説明した。ここまで３８分。
「まとめるとどうなるかな」
「じゃ、自分なりにまとめるとどうなるかな」このステップが大事だ。
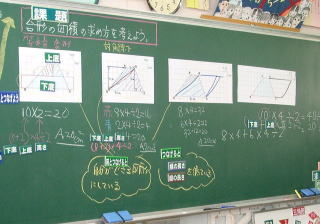
みんな、口々に自分の考えを唱える。
指名「台形の長さを求めるには、自分たちのできる図形に戻して、横の長さと縦の長さを使えばこ公式につなげられると思います。」
その後、教師は、「○○さんのがすごくいいと思う。みんなは、倍積変形、等積変形しようとしたけど、○○さんは、自分たちでできる形から求めようとした。」これは、直接公式につながらなかったが、その子独自に発想した方法を認めたものである。
「今まとめてくれたので、自分なりにまとめを書いてください。先生も書きます。」４１分経過。
教師は、「台形の面積も、自分たちが求められる図形に変形して、たての長さと横の長さを使って求めるとよい。」と板書した。児童はそれぞれ書いている。
一人の児童を指名して確認した後、練習問題に移った。その際にも、子どもたちは、口々に自分のやり方をあたかも宣言しているようだ。
活用問題として、ひし形の求積問題を一人の児童が指名された。明らかに誤解しており、行き詰まった。教師は、それでも、ぎりぎりまで声をかけない。そのタイミングは絶妙だった。すぐさま、すくいの声が飛び交う。「三角形の面積を求めて２倍すればよい。」一人の子が説明する。
「ひし形までは求められますね。終わりましょう。」
ここで係が前へ出る。一人の子を指名する。全員がその子の方を向く。
「今日は台形の面積を求める問題で、最初の方は分からなかったけど、みんなの話を聞いてわかったので、次やる時も、（上底＋下底）×高さ÷２ を使ってできるようになりたいです。」と振り返りの言葉を述べて終わった。
－ 感 想 －
以前驚いた、子ども同士の関わり合いの場面は今日はあまり見られなかった。課題の難しさ、それによる時間の不足が原因かと思ったが、渡辺先生は、後の研究協議で「個人の中である程度困難を乗り越えてほしい」その上で、「全体の中で他の子が乗り越えた壁を自分のものにしてほしい」と言われた。そのために、友達同士での話し合いにすぐに入らないで、個で取り組む時間を長くとったようである。十分理解できる。「学び合い」は美しいが、自ずから限界がある。最後は個の力が重要となる。渡辺学級はそこまで進化していた。
ここで、渡辺学級を中心に、今回の自分なりのまとめをしてみたい。研究要綱にこだわらない、自分なりの思いである。
（１）学び方の手順が明確に意識づけられている
授業記録の①から③は、まさに日頃のパターンである。児童が新たな事象に直面した時の手順が、どの子にも意識づけられている。ややくどすぎるほど、毎回の授業で繰り返されているのだろう。しかしそれが大事だ。
さらに、磁石がボード優れものである。やや多すぎる気もするが、慣れればよいのかも。問題解決のステップを意識するためには有効である。
（２）授業のポイントが明確である
本時は台形の面積を求めることが課題である。しかし、「これまでにわかっていることから考えること」「公式化（一般化）すること」ということが定着しているので、三角形や長方形、平行四辺形の学習の応用として位置づけられていることが明白である。従って、押さえどころが明確である。
（３）学び合いの姿勢が染みついている
これもパターンであるが、資料を見てすぐに話し合いが始まった。入学以来続けてきた学び合いは、すでに熟練の域に達している。何を言っても許されるという雰囲気が、子どもたちのバックにある。
（４）自己肯定感にあふれている
教師の発問に対して、挙手しながら「等積変形」「倍積変形」などと自分の論を主張する子どもたち。つぶやきながら、自分の考えを述べる子どもたち。これらは自分に自信があってこそ言える言葉である。答えが正しい、間違っているは問題ではなく、自分が何を言っても認められるという安心感。それは、自己肯定間につながってる。
授業のスタイルが、人格形成にまで影響を及ぼすとすると、それは重要だ。
ただし、心配な点もあった。
形式的に全員で大声を出すのは、時としてマイナスになるときもある。説明する子が「○○ですね。」というと「はい。」と条件反射的に言っているように聞こえる。一人ぐらい「待って」と言える余裕がほしい。型にはまることにより、学び方の習得や集中化には役立っているが、個の思考という点ではついて行けない子も出よう。小さなな声をいかに拾い上げるかが課題となろう。