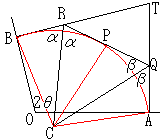
 左図のように△ABPの外心をCとすると,
左図のように△ABPの外心をCとすると,takahara さんの出題(それぞれ半直線に接し、互いに外接する2円)の解答
Q→Aのとき,P→A
R→Bのとき,P→Bだから,
A,Bも点Pの軌跡となる円周上にある。
すなわち,軌跡となる円は△ABPの外接円となる。
よって,任意の点Pに対して,△ABPの外接円は不変であることを示せば
点Pの軌跡はその外接円であると言える。
このためには△ABPの外心が点Pによらない定点であることを示せばよい。
 左図のように△ABPの外心をCとすると,
左図のように△ABPの外心をCとすると,
△ACQと△PCQについて,
AQ=PQ, AC=PC, CQ共通
∴△ACQ≡△PCQ
よって,∠AQC=∠PQC=βとする。
同様に,∠BRC=∠PRC=αとして,
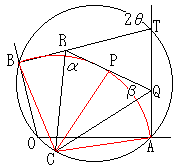 ∠AOB=2θとし,
∠AOB=2θとし,
直線AQ,BRの交点をTとすると,
∠OAT=∠OBT=90度だから,4点OATBは同一円周上にあり,
∠ATB=180度-2θ
よって,△TRQに対して,
(180度-2θ)+(180度-2α)+(180度-2β)=180度
∴θ+α+β=180度
このとき,
∠ACB=∠ACQ+∠QCP+∠PCR+∠RCB=2(∠QCP+∠PCR)=2θ=∠AOB
したがって,点Cは4点OATBを通る円周の弧AOB上のAC=CBとなる点である。
すなわち,点Cは点Pによらない定点である。![]()