が無理数である ことの証明（高校教科書に多くある例）

証明）

が無理数でない,つまり,有理数であると仮定すると,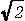は既約分数で表すことができる.

すなわち,互いに素な（1以外に公約数を持たない）整数a,bを使って,

と書ける。 これを平方整理して,

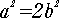
だから,a²は偶数,すなわちaは偶数となる. したがって,整数cを使って,

と書ける。 これを,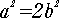に代入すると,

となり,b²は偶数,すなわちbは偶数となる. このとき, a,bは公約数2を持つことになり,1以外に公約数を持たないということと矛盾する。

この矛盾は最初に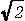が有理数であるとしたことが原因であり,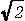は無理数である。