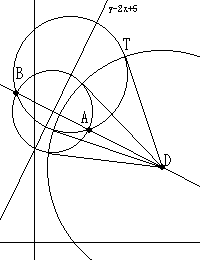
この問題は実は初等幾何の分野で解答するのが一番簡単で見通しがよい。
問題のポイントは直線ADと直線y=2x+5が直交することである。初等幾何のやり方でこの条件を書くと解答がわかってしまう怖れがある。そのため方程式などを使ってカムフラージュした。
出題者 takahara 自身による解答

円は直径に関して線対称だから,直線y=2x+5上のどのような中心に対しても,Aと線対称な点B(-1,8)も円周上の点であり、B,A,Dはこの順に一直線上に並ぶ.
方べきの定理より,![]()
よって, T,T'は点Dを中心とする半径![]() の円R上にある。
の円R上にある。
ただし,A,B,T,T'は同一円周上にあるので,T,T'は直線AB上にはない.
逆に A,B と円R上にあって直線AB上にない点T を通る円を考えると,
この円は必ず存在して,
円の中心はABの垂直2等分線 y=2x+5 上にあり,
方べきの定理より,DTは円Cに接する.
したがって,求める軌跡は円Rから直線ABとの交点をのぞいた図形.![]()